Data Structure: Binary Search Tree

BST

A Binary Search Tree (BST) is a binary tree in which the key stored at a node is greater than or equal to all the keys stored at the nodes of its left subtree and less than or equal to all the keys of its right subtree. This property is also called BST property.

Basic Operations

Key lookup, insertion and deletion all take time proportional to the height of the tree, which can be in the worst-case $O(n)$. However, for a height-balanced BST like Red-black tree, all these operations take $O(\log n)$.

As the min and max keys of a BST are respectively the leftmost leaf and the right most leaf, it takes time $O(h)$ to descend from the root to the leaves where $h$ is the height of the tree.

To iterate through all the elements of a BST in sorted order, we just need to do an inorder traversal of the binary tree itself. As each element is processed once, this operation takes time $O(n)$.

How to use BST

In practice, a BST can be used as a sorted hash table where the lookup takes time $O(\log n)$ for a library implementation. In python, the package bintrees provides Binary Red-Black and AVL-Trees. Another package sortedcontainers implements the sorted data structure as a sorted list of sorted lists where the insertion and deletion takes time $O(\sqrt n)$ asymptotically.

Red-Black Tree

A red-black tree is a binary search tree with one extra bit of storage per node: the color, either red or black. A red-black tree is balanced by constraining the node colors on any simple path from root to leaf.

B-tree

A B-tree is a generalization of BST in that a node can have more than two children. They are balanced search trees designed to work well on disks or other secondary storage devices. They are similar to Red-Black trees but better at minimizing disk I/O operations, so many database systems use B-trees.

If a node of B-tree has n sorted keys, then it has n + 1 children, the i-th key of the node serves as the separation point of the children i and i + 1. The number od children of a B-tree is also called the branching factor.

Secondary Storage

The main memory of a computer system normally consists of silicon memory chips, and the secondary storage are usually based on magnetic disk. The basic geometry of a modern disk is a platter together with a spindle/motor that drives the platter to spin at a constant rate, the typical rate for a modern disk in the 7200 rotations per minute (RPM) to 15 000 RPM range. For example, for a drive that rotates at 7200 RPM, the time that a single rotation takes is 8.33 ms.

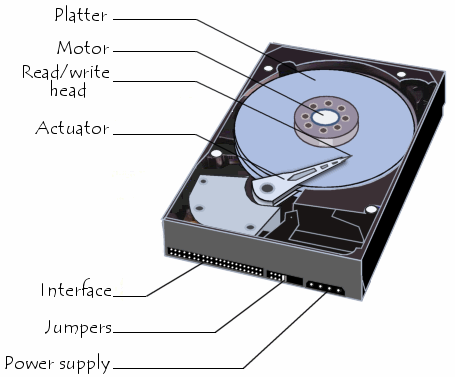
To read and write from the platter surface, we need a disk head connected to a disk arm to sense the magnetic pattern (read) or to induce a change (write) in it. As a typical disk I/O time is the sum of three components

$$T_{I/O} = T_{seek} + T_{rotation} + T_{transfer}$$

Typically for a disk of 7200 RPM, it takes 8 to 11 ms on average to access data (Ref. Introduction to Algorithms, 3rd edition), whereas the access time for main memory is around 50 ns, the latter can be 100000 times faster.

For a large B-tree stored on disk, the branching factor can be between 50 and 2000. A large branching factor can reduce the height of the tree efficiently, e.g. a branching factor of 1001 and height 2 can store over $10^9$ keys, and since the root node is permanently in main memory, it takes at most 2 disk accesses to find any key.